摘要
本文主要针对医院检验科从成本控制到人力调度的资源优化问题,基于附件所给数据 以及成本和工作效益的要求,建立基于LP-MIP的数学模型,实现了从微观检验项目优 化到宏观财务评估的全方位解决方案。
针对问题一,我们构建了以年利润最大化为目标的线性规划模型。该模型充分考虑 了检验科运营中的多种实际约束条件:首先,通过假定试剂的随机损耗率为5%来准确 计算实际成本;其次,针对不同检验项目的特点,设置了差异化的仪器使用约束(常 规项目1台,高频项目2台);最后,结合各检测小组的标本承载能力(门诊组15项/ 标本,免疫组20项/标本等),建立了严格的容量约束。模型求解结果显示,在优化检 测项目分配后,全年可实现总检测352,327次,创造总收入3783.06万元,其中试剂成 本占比控制在25%的合理范围内,最终实现净利润2839.34万元。通过对各检测小组 的成本利润结构分析,我们发现免疫组的肿瘤标志物检测和门诊组的甲乙流检测等项 目具有较高的利润贡献率,这为后续的重点项目推广提供了数据支持。详细数据见附 录2。
针对问题二,我们建立了考虑实际排班规则的整数规划模型。该模型创新性地将检 验科的特殊排班制度(每周工作4天、周末值班等)转化为数学约束条件,并引入了 人员处理能力的随机性(服从均匀分布)进行建模。通过建立0-1决策变量表示员工 排班状态,并设置人员调整变量来优化各小组配置,最终生成的排班方案不仅满足了 所有检测需求,还实现了人力成本的最小化。模型结果揭示了不同小组的人力配置不 均衡现象:门诊组存在明显的人员短缺,而免疫组则出现人力过剩的情况,这一发现 为医院的人力资源管理提供了重要参考。
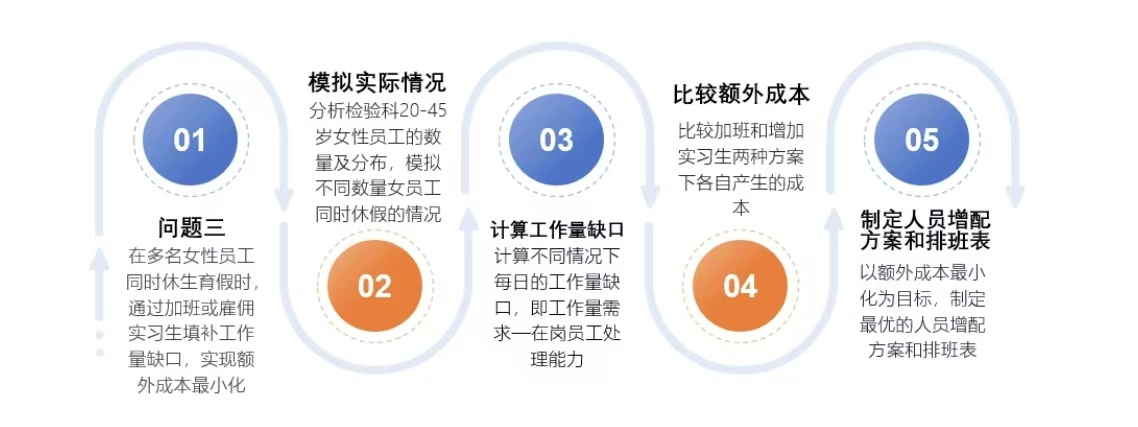
针对问题三,我们重点解决了生育假期间的人力资源调配难题。通过建立双层优化 模型,首先评估了不同休假人数情况下的工作量缺口,然后比较了现有员工加班和雇 佣实习生两种方案各自产生的额外成本。模型设置了严格的约束条件,包括每日工作 量必须完成、单月加班天数上限以及每组实习生雇佣人数上限。求解结果表明,当休 假人数增加时,采用混合策略(优先加班,不足时雇佣实习生)能够有效控制成本增 幅,在休假3人的情况下仍能保持成本增长在合理范围内(增幅7.46%)。这一研究 成果为医院应对突发性人力短缺提供了可行的解决方案。各组生育假排班表展示见图 26-图 29。
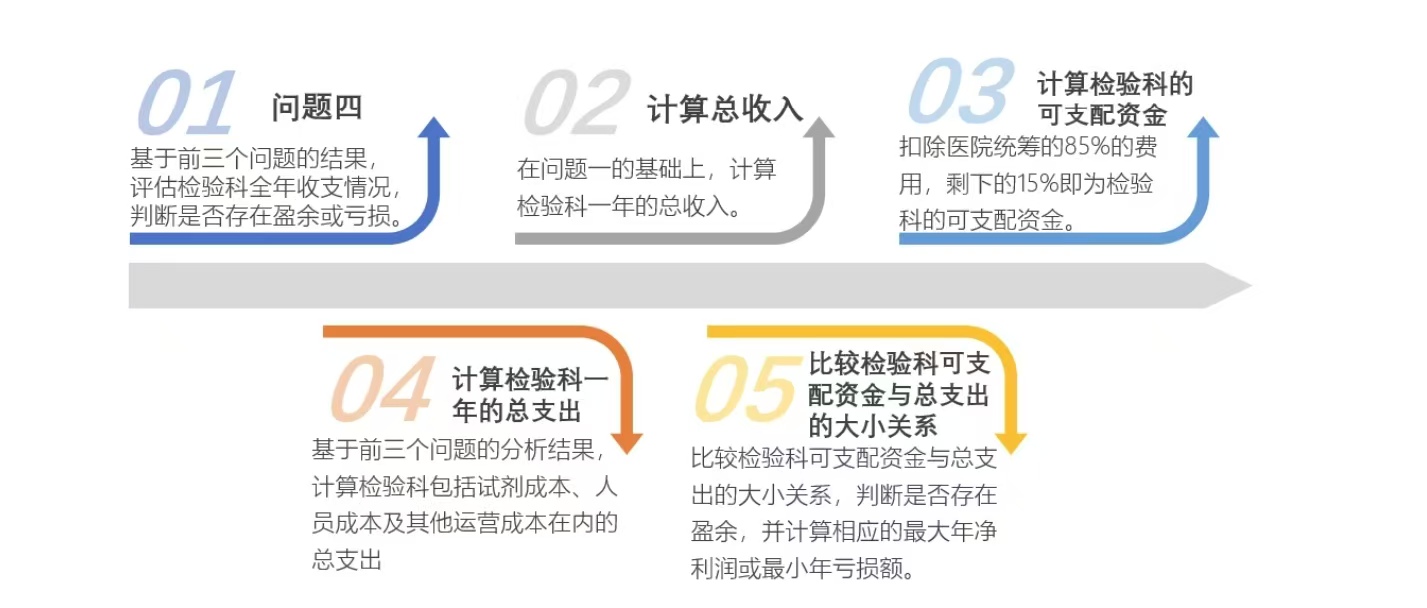
针对问题四,我们构建了完整的财务评估模型,系统分析了检验科的收支状况。该 模型创新性地将前三个问题的优化结果进行整合,通过建立收入分配函数(医院统筹 85%,检验科留存15%)和成本核算体系,准确评估了检验科的实际运营效益。灵敏 度分析显示,统筹比例的微小变动(±5%)会对盈余产生显著影响,这一发现对医院 的财务管理决策具有重要指导意义。求解结果表明,检验科整体处于盈利状态,且不 同检测小组的效益存在差异,其中免疫组的盈利能力最为突出。
本文模型通过线性规划和整数规划,实现了成本与人力配置的精细化优化,结果合 理且可验证。模型可推广至其他医院的科室管理,尤其适用于自负盈亏的运营场景。 未来可进一步纳入动态成本和非刚性约束,增强适用性。
关键词:医疗运营管理;线性规划模型;混合整数规划;资源优化配置
一、 问题重述
1.1 问题的背景
某大型综合医院的检验科由门诊组、免疫组、生化组和微生物组共4个小组构成,承 担全院的各类医学检测任务,不同时段的检验工作量受到多种因素的影响。科室采取自 负盈亏的运营模式,收入全部来自检测收费,支出包括试剂、人员及其他运营成本。
近年来,由于生活水平的提高,人们对健康体检的重视程度越来越高,检验仪器和专 业试剂的大量使用,使得医院的业务量和检验成本大幅度增加。随着我国医学类学科的 不断发展,医院间的竞争日益加大,医院若想适应当代市场需求,就必须加强科室成本 精细化管理。[1]因此,作为医院的核心部门,检验科需要对运营成本和人员配置进行优 化,实现人员最优配置。
1.2 问题的提出
根据题目背景和附件所给数据,我们需要解决以下问题:
1、基于附件所给数据,在每个月收入已知,人员成本和其他运营成本固定的条件下, 仅考虑试剂成本,进行合理性假设,建立以年利润最大化为目标的数学模型,从而确定 各组过去一年每个检验项目的检验数量,以及每个项目在过去一年的总收入,并结合实 际情况说明结果的合理性。
2、检验科各小组采用轮班制,每人每周在工作日工作 4 天,周六日和节假日每组保 留一名值班人员。为了让科室人员工作安排合理均衡,我们需要在问题1的基础上预估 今年6月份合理的检验项目数量,并建立数学模型,根据附件6所给数据,判断目前人 员数量及分组情况是否合理,根据结果进行人员增配,制定合理的6月份排班表。
3、针对检验科20~45岁女性员工可能同时休3个月带薪生育假的情况,在保证6月 份每日检验工作量完成的前提下,通过优化人员调配(现有员工加班或新增轮转医生/实 习生),制定成本最低的6月份人员增配方案,并给出合理的6月份排班表。
4、基于检验科收入分配比例,即医院统筹 85%,检验科留存 15%以支付包括日常运 营、检验工作保障及人员工资发放在内的所有开支,根据前面的分析结果,评估检验科 过去一年在扣除医院统筹费、支付所有开支后的盈余情况,若存在盈余,估算检验科的 最大年净利润,若存在亏损,估算在维持正常运营条件下的最小年亏损额。
二、 问题分析
2.1 问题一的分析
在月收入已知,人员成本及其他运营成本固定的条件下,仅考虑试剂成本,以年利 润最大化为目标建立数学模型,计算每个项目过去一年的检验数量和总收入,并结合 实际情况说明结果的合理性。 初步分析本问,已知年利润=总收入-总成本,其中总收入来自各项目的检测次数乘 以收费,成本包括试剂成本和其他损耗。
首先需要对每个标本能做的项目数量及试剂的各类损耗进行合理性假设,要想达到 目标,实现年利润最大化,需要在所做假设的基础上建立线性规划模型进行求解,[2]根 据我们需要求解的问题即计算每个项目在过去一年的检验数量和总收入,我们将每个 项目在不同月份的检测数量设置为决策变量,由于在使用Python对线性规划模型进行 2 求解时,只能求解模型的最小值,[3]因此我们将目标函数设置为全年试剂总成本的最小 值,并根据所给数据设置与收入和标本容量相关的约束条件,包括每个月的标本数限 制以及每个项目在仪器上的资源限制,以此保证在总收入固定的条件下,年利润达到 最大值。 在利用Python求得结果后,我们需要对模型进行检验,结合实际情况从每个月的总 收入、标本数容量以及模型的灵敏度多方面进行分析,判断所得结果是否符合预期、 是否合理。
具体流程图如下:
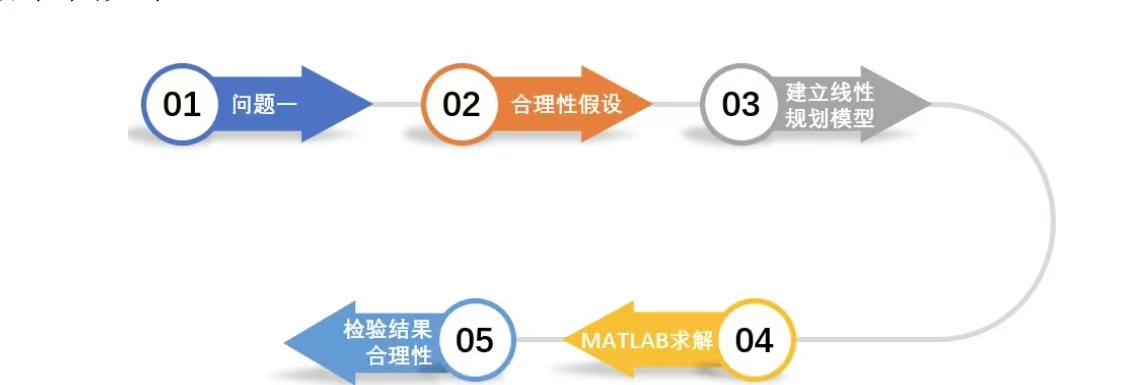
图一 问题一分析流程图
2.2 问题二的分析
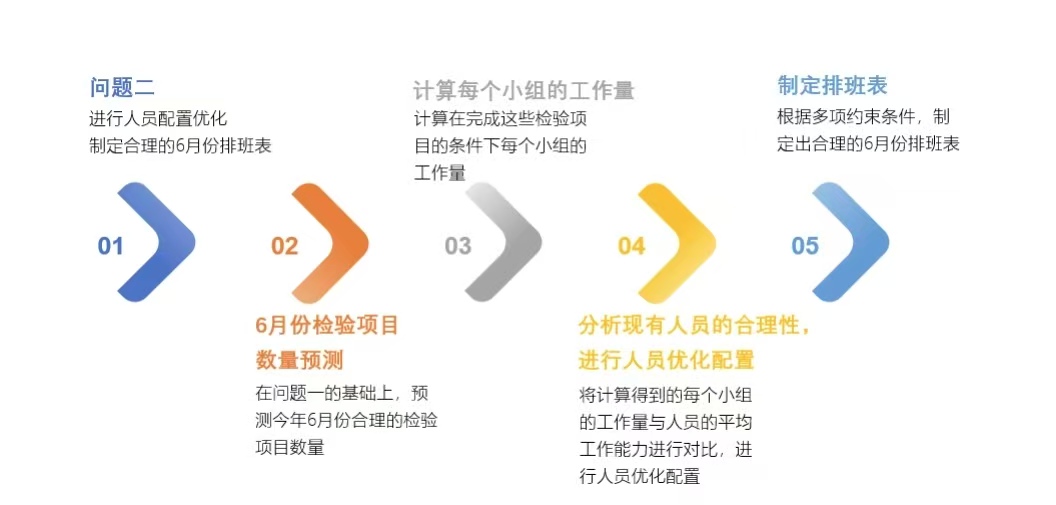
问题二需要我们在问题一的基础上,估计 6月份的检验项目数量,以降低人员成本、 提高效益为目标,分析人员配置是否合理,根据分析结果进行人员配置优化,制定合理 的6月份排班表。
在第一问的基础上,我们得到了6月份的检验项目数量。根据附件6所示的目前的人 员数量及分组情况,各小组实行轮班制(每周工作4天,周末节假日每组1人值班)。 我们需要计算每个小组的工作量,并与人员的工作能力进行对比。由于员工有不同的级 别,每天能处理的项目数量服从均匀分布,因此需要用期望值来计算平均处理能力。 基于得到的结果进行分析,如果人员富余,需要优化配置,减少人数;如果不足,则 需要增加人员。在此条件下制定合理的6月份排班表。 因此我们可以建立模型,根据需要解决的问题,我们分别设置0-1变量 日期d是否上班)和变量 (员工j在 (小组g需要调整的人员数量)为决策变量。为了降低人员 成本,我们将人员成本的最小值设定为目标函数。 排班表需要考虑每周的工作日安排,确保覆盖所有工作量,并均衡员工的工作量。据 此可对工作覆盖量、每周工作天数以及周末值班等条件进行约束。 综上所述,我们将采取整数规划来安排排班表,同时满足工作天数和休息要求。
具体流程图如下:
图二 问题二分析流程图
2.3 问题三的分析
在检验科多名20~45岁女性员工同时休3个月带薪生育假的情况下,我们需要通过 优化人员调配,制定6月份人员增配方案,并给出合理的6月份排班表,在保证6月份 每日检验工作量全部完成的同时,实现成本最小化。
在问题一和问题二的基础上,问题三考虑到女性员工休生育假的情况,我们假设休假 员工的工作处理能力直接扣除,为了保证检验工作能按时完成,工作量缺口需完全填补, 解决方案包括现有员工加班或雇佣实习生。
初步分析,在求解问题三时,首先需要了解检验科20-45岁女员工的数量和分布情况, 模拟不同数量员工同时休假的情况,计算不同情况下每日的工作量缺口,即工作量需求 —在岗员工处理能力。 接下来需要计算不同休假人数下的额外成本(加班工资或实习工资),比较加班和增 加实习生两种方案下各自产生的成本,从而给出成本最低的人员增配方案。
因此可以建立优化模型,根据需要解决的问题将0-1变量 加班)和变量 (员工 j 在日期 d是否 (小组 g在日期 d 雇佣的实习生数量)设置为决策变量,将额外成本 的最小值设为目标函数,约束条件包括工作必须全部完成、加班上限以及实习生雇佣上 限。在此条件下分析不同休假人数下的最优增配方法,并生成相应的排班表。
具体流程图如下:
图三 问题三分析流程图
2.4 问题四的分析
根据题目,医院会收取检验科年总收入的85%作为统筹费用,剩下的15%用于检验科 的日常运营。 问题四要求利用前三个问题的分析结果评估过去一年的收支情况,即扣除医院统筹 费85%后,检验科是否存在盈余。若存在盈余,我们需要估算检验科最大的年净利润; 若存在亏损,则需要估算在维持正常运营条件下的最小年亏损额。
初步分析,本问需要结合问题一所得的总收入,减去医院统筹的85%的费用,计算剩 余的15%是否足够支付所有开支。如果不足,则意味着出现亏损,需要计算最小亏损 额。 因此可建立数学模型,将“判断可支配资金与总成本之间的大小关系”作为目标函 数,同时还需要考虑实际医院运营的各种约束条件,进而评估检验科收支平衡状态, 并计算该状态下的最大年净利润或最小年亏损额。
具体流程图如下:
图四 问题四分析流程图
三、 模型假设
1、假设题目中给出的数据准确,无异常值。
2、假设人员工资、试剂成本及其他运营成本均为刚性支出,无弹性调整。
3、假设检验医师为不可调配岗位,不参与优化调配、加班或调岗。
4、假设解决问题时所使用的前面问题的计算结果准确无误。
四、 符号说明
表1 本文的符号说明

五、 模型建立与求解
5.1 问题一模型的建立与求解
5.1.1 模型的建立
问题一需要我们在给定各月收入与标本数的条件下,通过优化各检验项目的检测次 数分配,利用Python求解,使全年试剂成本最小化,实现年利润最大化。 因此可以建立线性规划模型,在对每个标本能做的项目数量及试剂的各类损耗进行 合理性假设的前提下,设置决策变量和目标函数,并明确问题的约束条件,以此对目 标函数进行求解。
对于问题一模型建立过程中使用到的临时参数,我们给出详细的参数定义及数据来源
我们假设每个标本在各组可检测的项目数 固定损耗按每月仪器数计算。 具体的线性规划模型建立过程如下:
(1)设置决策变量 为常数,试剂的随机损耗率 表3 模型一中的决策变量 恒为5%, 变量 含义 项目i在月份m的检测数量
(2)写出关键公式 每月固定损耗量: 此处 表示项目i的仪器数量,根据前面的合理性假设,常规项目默认使用1台仪器, 高频项目(如血常规)使用2台仪器。 作日天数固定为22天。 表示月份m的工作日天数,我们假设每月工 7 需要注意的是,每日质量控制消耗2个试剂 × 工作日22天,每月定标试剂(取中间 值5个)和校准试剂1个,共 2×22+5+1=502×22+5+1=50 个试剂/月/仪器。若项目使用 多台仪器(如 =2),则损耗翻倍。 单位试剂总成本(含随机损耗):
(3)建立目标函数 此处固定损耗量
(4)设置约束条件 ① 收入约束:各组各月检测收入等于给定值: ② 标本容量约束:检测总数不超过标本承载能力: ③ 非负性约束: 由此可得,约束条件为:
(5)模型检验与预期结果 表4 模型一的检验方法与预期结果 检验方法 操作 预期结果 收入验证 容量验证 敏感性分析 检查每个月的总收入是否 严格等于 确保 误差为0 所有月份检测次数未超 限 调整随机损耗率 β(±2%) 总成本波动幅度与损耗 率变化一致
5.1.2 模型的求解
(一)数据预处理
(1)门诊组数据清洗过程 图5 门诊组数据清洗过程
(2)免疫组数据清洗过程 图6 免疫组数据清洗过程
(3)生化组数据清洗过程 图7 生化组数据清洗过程
(4)微生物组数据清洗过程 9 图8 微生物组数据清洗过程
(二)代码求解思路(部分代码展示) 模型一求解的部分代码展示,完整代码见附录3。 图9 模型一部分代码展示
5.1.3 模型的结果分析
(一)整体概况 指标 表5 检验科工作年度概况 数值 说明 年度总检测次数 年总收入(万元) 试剂总成本(万元) 年净利润(万元) 352327 次 3783.0578 943.7168 2839.3412 全科室全年完成的检验 项目总数,反映整体业 务规模。 各项目收费总和,体现 检验科创收能力。 固定损耗(质量控制、 定标)和可变损耗(随 机损耗)的总和,占收 入的25%。 总收入 - 试剂成本,显 示检验科盈利能力(仅 考虑试剂成本的情况 下)。
(二)关键项目分析
(1)门诊组
① 关键项目:甲乙流、便潜血、α-淀粉酶(α-AMY)
② 图表分析:甲乙流项目的利润占比最高,显示出其在门诊组中的重要性。便潜血和 α-淀粉酶项目的成本与利润占比相对均衡。
③ 建议:加强对甲乙流检测的推广,尤其是在流感高发季节。便潜血和α-淀粉酶项目 可以进一步优化成本,以提升其利润率。
(2)免疫组
① 关键项目:肿瘤标志物系列(肿瘤标志物2、肿瘤标志物1、肿瘤标志物3)
② 图表分析:肿瘤标志物2的利润占比远高于成本占比,显示出其高效的盈利能力。 其他肿瘤标志物项目也表现出较好的利润贡献。
③ 建议:继续推广肿瘤标志物检测,同时优化成本结构,以进一步提升利润率。
(3)生化组
① 关键项目:心肌检测、底物类、酶类
② 图表分析:心肌检测项目的利润占比最高,显示出其在生化组中的重要性。底物类 和酶类项目的成本与利润占比相对均衡。
③ 建议:支持心肌检测项目的发展,并寻找进一步降低成本的方法,以提高底物类和酶 类项目的利润率。
(4)微生物组
① 关键项目:药敏(上机方法)、真菌培养、艰难梭菌抗原+毒素
② 图表分析:药敏项目的利润占比显著高于成本占比,表明其在微生物组中的核心地 位。艰难梭菌项目尽管成本较低,但利润贡献较小。
③ 建议:加强对药敏项目的资源投入,并探索提高艰难梭菌项目检测频率的方法。
(三)成本结构分析
(1)高利润、低投入的项目
① 信息:某些项目的利润占比明显高于其成本占比,表明这些项目在较低的成本投入 下产生了较高的利润。例如,免疫组中的“肿瘤标志物”系列项目显示出较高的利 润占比。
② 建议:可以考虑增加这些高利润项目的检验次数或推广这些项目,以进一步提升整 体利润。同时,优化资源配置,将更多资源倾斜到这些高效益项目上。
(2)高成本、低利润的项目
① 信息:部分项目的成本占比远高于其利润占比,意味着这些项目可能需要较高的成 本投入,但回报相对较低。例如,微生物组中的某些培养类项目显示出较高的成本 占比但利润较低。
② 建议:对于这些项目,建议进行详细的成本分析,寻找降低成本的方法,或者评估 是否有必要继续大规模投入。如果这些项目对业务的战略意义不大,可能需要减少 其资源分配。
(3)季节性或需求波动的项目
① 信息:通过结合月度详情数据,可以观察到某些项目的检验次数在不同月份有显著 波动,这可能与季节性需求或特定时期的疾病高发有关。
② 建议:针对这些项目,建议进行需求预测和灵活的资源配置,以应对季节性波动。 同时,可以考虑在需求高峰期前进行市场推广,进一步提升检验量。
(4)收入结构的优化
① 信息:从收入占比和利润占比的对比中,可以看到某些高收入项目并未带来相应的 高利润,可能存在成本控制问题。
② 建议:建议对这些高收入项目进行成本结构的详细分析,找出成本高的原因,并采 取措施优化成本,如改进流程、谈判更好的供应链价格等。
(四)合理性检验
(1)收入差异平均值 门诊组、免疫组、生化组和微生物组的收入差异平均值都非常接近6.05%,这表明在 13 不同组别中,收入计算方法是一致的,且数据的合理性较高。
(2)每个标本检验数分析 各组平均每标本检验数 系列1 0 1 2 3 4 5 4.04 0.48 1.72 1.45 门诊组 免疫组 生化组 微生物组 图15 各组平均每标本检验数 门诊组的平均每标本检验数最高,为4.04,显示出每个标本的检验次数较多,可能 与该组的检验项目种类和复杂性有关。 免疫组的平均每标本检验数最低,为0.48,表明该组的检验项目可能较为单一或标 本使用率较低。 生化组和微生物组的平均每标本检验数分别为1.72和1.45,处于中等水平。
5.2 问题二模型的建立与求解
5.2.1 模型的建立
问题二需要我们在问题一的基础上,估计6月份的检验项目数量,并计算在完成这些 检验项目的条件下每个小组的工作量。以降低人员成本、提高工作效益为目标,将每个 小组的工作量与人员的工作能力进行对比,分析人员配置是否合理。 需要注意的是,在计算员工的工作能力时,由于员工有不同的级别,每天能处理的项 目数量服从均匀分布,因此需要用期望值来计算平均处理能力。 根据分析结果进行人员配置优化,如果人员富余,需要优化配置,减少人数;如果不 足,则需要增加人员。 根据上述结果制定合理的6月份排班表。排班表需要考虑每周的工作日安排,确保覆 盖所有工作量,并均衡员工的工作量。据此可对工作覆盖量、每周工作天数以及周末值 班等条件进行约束。我们采取整数规划来安排排班表,同时满足工作天数和休息要求等 约束条件。
对于问题二模型建立过程中使用到的临时参数,我们给出详细的参数定义及数据来 源: 表6 模型二中的参数定义及数据来源 符号 含义 数据来源(计算方法) 小组 g在6月的预估检 验项目总数 基于问题1的模型预测 或历史数据(如附件1 14 中往年6月数据) 小组 g 在日期 d需完成 的检验项目数 6 月工作日天数 员工 j的日处理能力(项 /天) 工作日(周一至周五) 占90%工作量,周末占 10% 假设6月有22个工作 日,8个周末/节假日 根据职级:初级50(均 匀分布期望值)、中级 70、高级90、检验医师 70 员工 j 的月薪(元) 检验医师10000元,高 级技师10000元,中级 8000 元,初级7000元 小组 g的现有人员数量 及职级分布 附件6中按小组、职级 分类统计 每人每月最多工作天数 按每周4天计算,6月约 工作 4×4=164×4=16 天 周末每日每组需至少1 人值班 约束条件 我们假设工作日占90%的工作量,周末占10%,均匀分配到每日。除此之外,检验医 师必须保留,且不参与优化调整。
具体模型建立过程如下:
(1)设置决策变量 表7 模型二中的决策变量 变量 含义 员工 j 在日期 d 是否上班(0-1变 量,1表示上班) 小组 g需调整的人员数量(正值为 增员,负值为减员)
(2)写出关键公式 每日工作量分配: 总人力需求(按处理能力计算):
(3)建立目标函数 最小化人力成本(工资+加班/实习成本): 此处为调整成本系数(增员:实习工资100元/天;减员:裁员成本暂忽略)
(4)设置约束条件 ① 工作覆盖量: ② 每周工作天数: “ ”指的是第k周,而“d”代表日期(天) ③ 周末值班: ④ 人员调整范围: ⑤ 不可裁员约束:检验医师数量 由此可得,约束条件为: 当前数量 5.2.2 模型的求解 模型二求解的部分代码展示,完整代码见附录4。 图16 模型二部分代码展示
5.2.3 模型的结果分析
(一)人员需求与人力平衡情况分析 图17 工作日人员需求与人力平衡 图18 周末人员需求与人力平衡 从图中可知:
(1)门诊组:工作日需求远高于实际人力配置,存在明显的人员短缺。周末需求相对 较低,但同样存在人员不足的情况。
(2)免疫组: 工作日和周末的需求都较低,且实际人力配置超过了需求,存在人员过剩的情况。
(3)生化组: 工作日需求较高,但实际人力配置略显不足。周末需求相对较低,人力配置基本满足 需求。
(4)微生物组: 工作日和周末的需求都较低,实际人力配置能够满足需求,且略有富余。 626.49 163.46 427.11 132.9-170.49 172.54-35.11 131.1-400-200 0 200 400 600 800 9 6 7 5 工作日人员需求与人力平衡 工作日需求工作日人力平衡 162.42 42.38 110.73 34.46-92.42 27.62-40.73 35.54-150-100-50 0 50 100 150 200 9 6 7 5 周末人员需求与人力平衡 周末需求周末人力平衡
(二)排班情况分析
(1)门诊组排班 图19 门诊组6月排班情况 从热力图中可以看到,门诊组的排班在工作日和周末之间存在明显的差异。工作日 的排班密度较高,而周末的排班相对较少。这反映了门诊组的工作量在工作日较高, 而在周末有所下降。
(2)免疫组排班 图20 免疫组6月排班情况 免疫组的排班显示出一定的规律性,部分员工在特定日期连续多天排班,而其他日 期则没有排班。这表明免疫组的任务具有周期性,或者某些员工专门负责特定日期的 工作。
(3)生化组排班 18 图21 生化组6月排班情况 生化组的排班情况显示出较高的均匀性,员工在整个月内都有较为均衡的排班,反映 了生化组工作任务的持续性和稳定性,没有明显的高峰或低谷。 (4)微生物组排班 图22 微生物组6月排班情况 微生物组的排班显示出一定的集中性,部分员工在特定周内有密集的排班,而其他 周则相对空闲。这与微生物组的工作任务性质有关,可能需要在特定时间段内集中处 理某些任务。
(三)排班合理性分析
(1)工作负荷均衡性:从热力图可以看出,不同小组的排班密度和分布存在差异并不 显著。各组的排班显示都较为均衡,说明排班表具有工作负荷均衡性,有利于提高整体 工作的可持续性。
(2)任务需求匹配性:各组的排班安排与其工作任务的需求相匹配。如门诊组在工作 日的排班密度较高,符合门诊工作量在工作日较大的特点。
(3)灵活性与适应性:免疫组和微生物组的排班显示出一定的灵活性,能够根据任务 需求进行调整。这种灵活性是合理的,可以更好地应对突发任务或特殊项目的需求。
5.3 问题三模型的建立与求解
5.3.1 模型的建立
在检验科多名20~45岁女性员工同时休3个月带薪生育假的情况下,我们需要通过 优化人员调配,制定6月份人员增配方案,并给出合理的6月份排班表,在保证6月份 每日检验工作量全部完成的同时,实现额外成本最小化。 因此可以建立优化模型,以实现额外成本最小化为目标,给出成本最低的人员增配方 案。 对于问题三模型建立过程中使用到的临时参数,我们给出详细的参数定义及数据来 源:表8 模型三中的参数定义及数据来源
我们假设每名休假员工的工作处理能力直接减少,缺口需完全填补,实习生的每日工 作处理能力与初级技师相同,均为50项/天。我们规定采用优先级策略,即优先使用现 有员工加班,现有员工不足时再雇佣实习生。 具体的优化模型建立过程如下:
(1)设置决策变量
(2)写出关键公式 每日工作量缺口: 若 ,需要通过加班或实习生填补
(3)建立目标函数 最小化额外成本(加班工资+实习工资):
(4)设置约束条件 ① 工作量覆盖: ② 加班限制: ③ 实习生数量限制: ④ 排班均衡性: 由此可得,约束条件为:
5.3.2 模型的求解
模型三求解的部分代码展示,完整代码见附录5。 图23 模型三部分代码展示
5.3.3 模型的结果分析
(一)休产假人数与平均总成本分析 22 休产假人数与平均总成本的关系 系列1 16000 15000 14000 13000 12000 11000 12971.43 14137.14 15191.88 1 2 3 图24 休产假人数与平均总成本的关系 图表展示了休产假人数与平均总成本的关系,随着休产假人数的增加,平均总成本 呈现上升趋势。 平均总成本随产假人数变化的增减 幅度 1~2 2~3 10 0 2 4 6 8 8.99 7.46 图25 平均总成本随产假人数变化的增减幅度 当休产假人数从1人增加到2人时,平均总成本增加了约8.99%。当休产假人数从2 人增加到3人时,平均总成本增加了约7.46%。这表明随着休产假人数的增加,平均 总成本的增长幅度有所放缓。 结合二者可知:当休产假人数增加时,虽然总成本在上升,但增幅逐渐减小。说明 本模型生成的排班结果具有合理性,在满足工作量的情况下有效降低成本。
(二)各组排班表展示 经过计算,可得各组生育假增配方法如下(表中○表示休息,□表示工作):
(1)门诊组 23 图26 门诊组生育假排班表
(2)免疫组 图27 免疫组生育假排班表
(3)生化组 图28 生化组生育假排班表
(4)微生物组 图29 微生物组生育假排班表
(三)排班表合理性分析 图30 各组各日期工作密度 24 由图可知: 工作密度具有稳定性:大部分日期的工作密度保持在相对稳定的水平(例如10到11 之间),这表明排班安排在大多数情况下是均衡的,且整体工作密度较为稳定,说明在 仅考虑成本问题的情况下,针对各种可能的同时休生育假的人数,今年6月份的人员排 班表具有合理性
5.4 问题四模型的建立与求解
5.4.1 模型的建立
根据题目,医院会收取检验科年总收入的85%作为统筹费用,剩下的15%用于检验科 的日常运营。 问题四要求利用前三个问题的分析结果评估过去一年的收支情况,即扣除医院统筹 费85%后,检验科是否存在盈余。若存在盈余,我们需要估算检验科最大的年净利润; 若存在亏损,则需要估算在维持正常运营条件下的最小年亏损额。 根据问题一所得的检验科年总收入,扣除85%医院统筹费用后可得检验科的可支配资 金,计算这一年里检验科的总成本即包括试剂成本、人员成本及其他运营成本在内的 总支出,比较可支配资金与总成本之间的大小关系,据此可知检验科一年的盈余情 况。
因此可建立数学模型,将“判断可支配资金与总成本之间的大小关系”作为目标函 数,同时还需要考虑实际医院运营的各种约束条件,进而评估检验科收支平衡状态, 并计算该状态下的最大年净利润或最小年亏损额。 对于问题四模型建立过程中使用到的临时参数,我们给出详细的参数定义及数据来 源: 表10 模型四中的参数定义及数据来源 符号 含义 数据来源(计算方法) 检验科年总收入(万元) 问题1中各项目年总收 入的累加和 全年试剂总成本(万元) 问题1中计算的试剂成 本(固定损耗 + 可变损 耗) 全年人员工资总成本 (万元) 基于附件6或问题2优 化后的配置,按职级月 薪×12计算 其他运营成本(万元) 固定为4万元/月 ×12 = 48 万元 年净利润(万元) 年亏损额(万元) 若可支配资金 ≥ 总成 本,盈余=可支配资金 - 总成本 若可支配资金 < 总成 本,亏损=总成本 - 可支 25 配资金 医院统筹费用比例 85% 我们假设人员工资、实际成本以及其他运营成本均为刚性支出,无弹性调整,且不考 虑突发情况(如生育假)导致的额外成本。
具体的模型建立过程如下:
(1)建立目标函数 评估检验科收支平衡状态: 目标:判断可支配资金≥总成本
(2)设置约束条件 ① 收入与成本定义: ② 统筹费用扣除: ③ 成本汇总: ④ 盈余/亏损判断: 由此可得,约束条件为: 5.4.2 模型的求解 模型四求解的部分代码展示,完整代码见附录6。 26 图31 模型四部分代码展示
5.4.3 模型的结果分析
(一)整体收支概况
(1)检验科年度财务概况 净利润/亏损 年总支出 年其他运营成本 年试剂成本 年人力成本 检验科可支配收入(... 医院统筹费(85%... 检验科年度财务概况 1023146 4327714 480000 943714 2904000 5350860 年总收入 0 10000000 20000000 30000000 图32 检验科年度财务概况 由图可知: 系列1 30321540 35672400 40000000
①年总收入为 35,672,400 元,其中医院统筹费占比 85%,即30,321,540元,而检验科 可支配收入为15%,即5,350,860元。
②年总支出为43,277,14元,主要包括年人力成本(29,040,00元)、年试剂成本(9,437,14 元)和年其他运营成本(4,800,00元)。
③问题四的求解答案为:最终的净利润为10,231,46元,表明检验科在扣除所有成本后 仍保持盈利状态。
(2)各组别年总收入、年总成本和净利润对比 27 各组别年总收入、年总成本和净利润对比 16000000 14000000 坐标轴标题 12000000 10000000 8000000 6000000 4000000 2000000 0 年总收入 年总成本 14895140 9080675 1193753.25 168348 门诊组 9062164 1746192 1128577.6 2634421 488079 230747 56540 免疫组 生化组 338623.15 微生物组 9080675 14895140 9062164 168348 488079 2634421 230747 净利润/亏损 1193753.25 1746192 56540 1128577.6 338623.15 图33 各组别年总收入、年总成本和净利润对比 由图可得结论:
① 免疫组的年总收入最高,同时其年总成本也相对较高,但净利润仍然是所有组别中 最高的。
② 门诊组的年总收入次之,净利润也较为可观。
③ 生化组的年总收入与门诊组相近,但其净利润略低。
④ 微生物组的年总收入和净利润都是最低的,说明其运营规模相对较小。
(二)月度盈亏情况分析
检验科月度盈亏情况 250000 200000 150000 100000 50000 0 216339.07 86196.52 187383.67 105270.07 27781.42 125476.42 96432.97 90872.92 67937.62 8620.27 2095.72 8739.37 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月 系列1 图34 检验科月度盈亏情况 由图可得:
① 3月是盈利最高的月份,盈亏金额达到216,339.07元。
② 其他月份的盈亏金额相对较为平稳,但10月和11月的盈利金额明显较低,分别为 8,620.27 元和 2,095.72 元。
③ 月度平均盈亏金额为85,262.17元,表明检验科在每个月的平均盈利情况较为稳 定。
④ 收支平衡所需月收入为24,042,855.56元,这意味着检验科每月需要达到这一收入 水平才能实现收支平衡。 整体来看,检验科在全年12个月中均保持了盈利状态,没有出现亏损的情况。
(三)成本占比分析
(1)各组别年试剂成本占比
① 各组别年总收入对比:从柱状图可以看出,免疫组的年总收入最高,远超其他组 别,而微生物组的年收入最低。
② 各组别净利润对比:净利润的柱状图显示,免疫组的净利润同样最高,而微生物 组的净利润最少,但所有组别均处于盈利状态。
③ 各组别年试剂成本占比:饼图展示了各组别年试剂成本的占比情况,免疫组和生 化组的试剂成本占比较大,而门诊组和微生物组的试剂成本相对较低。
(2)各职级年总成本占比 图36 各职级年总成本占比
① 检验医师的年总成本为18,000,000元。
② 中级检验技师的年总成本为7,680,000元。
③ 初级检验技师的年总成本为3,360,000元。
可以看出,检验医师的年总成本远高于其他职级,这与其人数和薪资水平较高有关。 168348, 18% 488079, 52% 230747, 24% 56540, 6% 各组别年试剂成本占比 门诊组免疫组生化组微生物组 检验医师, 1800000, 62% 中级检验技师, 768000, 26% 初级检验技师, 336000, 12% 各职级年总成本占比 检验医师中级检验技师初级检验技师
(3)各职级占总人力成本比例
① 检验医师占总人力成本的比例为61.98%。
② 中级检验技师占总人力成本的比例为26.45%。
③ 初级检验技师占总人力成本的比例为 11.57%。
这些数据表明,检验医师的人力成本占据了检验科总人力成本的绝大部分,而中级和 初级检验技师的成本相对较低。
(4)检验科成本结构占比 检验科成本结构占比 试剂成本 21.81 22% 其他运营成 本 11.09 11% 人力成本试剂成本 人力成本 67.1 67% 其他运营成本 图38 检验科成本结构占比
① 年人力成本占总支出的约67.1%。
② 年试剂成本占总支出的约21.8%。
③ 年其他运营成本占总支出的约11.1%。
从图中可以看出,人力成本是检验科最大的支出项,其次是试剂成本和其他运营成 本。
(四)总结
(1)检验科整体处于盈利状态:检验科在全年中保持了持续的盈利,没有出现亏损的情 况。
(2)盈利额占可支配收入的比例:当前的盈利额占检验科可支配收入的19.12%,表明 仍有提升空间。
(3)全年盈利情况:全年12个月均为盈利状态,没有出现亏损的月份,财务状况较为 稳定。
(4)最佳盈利月份:3月份是盈利最高的月份,盈利额达到216,339.07元,表明该月的 运营效率较高。
(5)各组别盈利情况: 门诊组盈利1,193,753.25 元。 免疫组盈利1,746,192.00 元,为各组别中盈利最高的组别。 生化组盈利1,128,577.60 元。 微生物组盈利338,623.15元。
六、 模型检验
6.1 问题一中的模型灵敏度分析 表11 关键参数变化对模型一结果的影响 参数 变化范围 对总成本的影响 对检测次数分配的 影响 随机损耗率( 样本容量( ) ±2%(3% ~ 7%) ) ±5项/标本 工作日天数 ↑2%:总成本增 加约4.2%。 ↓2%:总成本减 少约3.8%。 ↑5:总成本下 降(因允许更多检 测次数摊薄固定损 耗)。 ↓5:总成本上 升 ↑2:固定损耗 () ±2天(20 ~ 24 天) 成本增加约4%(因 检测次数分配不变 (因收入约束固 定),但单位试剂 成本变化影响总利 润 检测次数可能重新 分配,高利润项目 优先增加,低利润 项目减少。 检测次数分配需调 整以满足收入约 31 质量控制试剂消耗 增加)。 ↓2:固定损耗 成本减少约3.6%。 仪器数量() ±1台(特殊项 目) ↑1:固定损 耗成本翻倍。 ↓1:固定损 耗成本减半。 束,可能压缩低利 润项目。 高频项目(如血常 规)的检测次数可 能减少,以补偿成 本上升。
6.2 问题二中的模型灵敏度分析 表12 关键模型参数变化对模型二结果的影响 参数 变化范围 对人员影响的配置 对总成本的影响 每日工作量分布 工作日:周末=85%:15% 周末需求↑:需增加 周末值班人员或实习 生,可能需增配1~2 人。 员工处理能力() ±10%(初级45~55项 /天) 人员调整成本( 处理能力↓10%:需 增配1~2名初级技师 或实习生。 处理能力↑10%:可 减少1名初级技师。 ) ±20% 增员成本↑:更倾向 于减少裁员,保留现 有人员。 减员成本↓:优化后 可能裁员更多 最大加班天数 () ±2天(6~10天) 加班天数↑:减少实 习生雇佣量,节省实 习成本。 成本上升约3%~5% (因实习生或加班增 加)。 成本波动幅度约±8% (处理能力与人力需 求成反比)。 总成本变化幅度与调 整方向相关(增员时 影响显著,减员时影 响较小)。 成本波动约±5%(加 班工资与实习工资差 异影响结果)。 32 加班天数↓:需增配 实习生填补缺口。 6.3 问题三中的模型灵敏度分析 表13 关键参数变化对模型三结果的影响 参数 变化范围 对应策略的影响 对总成本的影响 每日工作量缺口 加班工资( ±20% ) ±50元/天 (150~250 元) 实习生处理能力 ±10项/天(40~60 项) 最大加班天数 () 缺口↑20%:需额外 增加1~2名实习生 或延长加班天数。 缺口↓20%:可减少 实习生雇佣或加班 天数。 加班工资↑:优先 雇佣实习生,减少 加班天数。 加班工资↓:更多 依赖加班。 能力↓10项:需多 雇佣1名实习生填 补相同缺口。 能力↑10项:减少 实习生需求。 ±2天(6~10天) 加班天数↑:减少 实习生雇佣,节省 实习成本。 加班天数↓:需增 配实习生。 实习生雇佣上限 () ±1人(2~4人) 上限↑1人:可降 低加班需求,成本 下降5%~10%。 上限↓1人:被迫 增加加班,成本上 升5%~15% 成本波动约± 15%~25%(缺口与 成本线性相 关)。 若全部缺口由加班 填补,成本变化± 10%;若由实习生填 补,影响较小(± 5%) 成本波动约±20% (处理能力与实习 生数量成反比)。 成本波动约±8% (取决于缺口大小 与实习生雇佣比 例)。 成本受策略切换影 响显著,尤其在高 峰日。 33 6.4 问题四中的模型灵敏度分析 表14 关键参数变化对模型四结果的影响 参数 变化范围 对盈余/亏损的影 响 敏感度等级 年总收入( 试剂成本 () 人员工资( ) ±10%(2700~3300 万元) ±10%(162~198 万 元) ) ±20%(160~240万 元) 医院统筹比例 ( ) ±5%(80%~90%) 统筹比例↑5%:可 支配资金-150万 高 收入↑10%:可支 配资金+45万元, 总成本不变,盈余 增加45万元。 收入↓10%:可支 配资金-45万元, 若原盈余22万元, 转为亏损23万元 成本↑10%:总成 本+18万元,原盈 余22万元降至4万 元。 成本↓10%:总成 本-18万元,盈余 增至40万元。 工资↑20%:总成 本+40万元,原盈 余22万元转为亏损 18 万元。 工资↓20%:总成 本-40万元,盈余 增至62万元。 元,原盈余22万元 转为亏损128万 元。 统筹比例↓5%:可 支配资金+150万 元,盈余增至172 万元 中 高 极高 34 其他运营成本 () 低 ±20%(38.4~57.6 万元) 成本↑20%:总成 本+9.6 万元,盈余 降至12.4万元。 成本↓20%:总成 本-9.6 万元,盈余 增至31.6万元。
七、 模型优缺点评价
7.1 模型的优点
① 本文的模型建立在理性的分析和合理的推导之上,目标明确,约束条件清晰,通过 建立线性规划模型,实现成本最小化,工作效益最大化。模型的建立整体且全面, 求解效率高,复杂度可控,结果较为准确,一目了然。
② 模型的建立严格依赖附件数据(收入、试剂价格),结果可验证。
③ 该模型对于本文给出的医院检验科运营优化问题,有着较强的实用性和适用性,随 着检验项目数量的改变依然可以使用,具有较强的现实意义。
7.2 模型的缺点
① 在建立模型的过程中,我们假设成本为刚性支出且无弹性调整,忽略了市场波动、 政策调整等动态因素。
② 在解决问题的过程中,依赖前置模型,若前一个问题的输入数据存在误差,结果将 直接传至下一个问题,误差可能被放大。
参考文献
[1] 张金宝. TDABC在A医院检验科成本管理应用研究[D]. 安徽财经大学, 2021. DOI:10.26916/d.cnki.gahcc.2021.000601.
[2] 秦晓薇. 线性规划模型的应用研究 [J]. 赤峰学院学报(自然科学版), 2012, 28 (08): 30-31. DOI:10.13398/j.cnki.issn1673-260x.2012.08.110.
[3] 张颖. 线性规划模型中Python的求解实现 [J]. 通化师范学院学报, 2009, 30 (12): 13-14+17.
附录 附录1 介绍:支撑材料的文件列表
附录2 介绍:问题一求解结果 门诊组: 37 免疫组: 38 生化组: 微生物组: 39
附录3 介绍:部分Python代码展示,用于求解模型一(完整代码位于支撑文件) import numpy as np import pandas as pd from scipy.optimize import linprog import pulp as pl # 初始化数据 group_names = ["门诊组", "免疫组", "生化组", "微生物组"] months = 12000 # 每月标本数和收入 (正确的数据格式) monthly_data = { "门诊组": { "标本数": [11957, 13066, 19607, 14608, 16579, 14618, 13976, 13916, 13743, 13842, 12259, 12515], "总收入": [741790, 628135, 1113670, 752810, 877650, 771250, 717200, 686810, 705550, 713250, 608170, 764390] }, "免疫组": { 40 "标本数": [5708, 7326, 8686, 7348, 8851, 7873, 7484, 7597, 7140, 6094, 6790, 6012], "总收入": [889290, 1355680, 1545000, 1336530, 1620690, 1408420, 1307230, 1323580, 1218260, 986550, 1024960, 878950] }, "生化组": { "标本数": [5824, 6085, 7385, 6115, 6868, 6369, 5814, 6140, 5897, 3653, 5017, 4861], "总收入": [751544, 801217, 943942, 791859, 905567, 800534, 771619, 761847, 727488, 587786, 591297, 627464] }, "微生物组": { "标本数": [2153, 1756, 2331, 2031, 2377, 2495, 2334, 2184, 1937, 1508, 1736, 1862], "总收入": [206871, 193897, 243934, 224887, 249603, 260591, 251123, 237868, 205905, 174168, 193830, 191744] } }
附录4 介绍:部分Python代码展示,用于求解模型二(完整代码位于支撑文件) import numpy as np import pandas as pd from datetime import datetime, timedelta import calendar import random # 1. 数据准备 # 员工数据 staff_data = { 'id': list(range(1, 28)), 'position': [ '检验医师', '检验医师', '检验医师', '检验技师', '检验医师', '检验技师', '检验 医师', '检验技师', '检验医师', '检验技师', '检验技师', '检验医师', '检验医师', '检验 医师', '检验医师', '检验技师', '检验技师', '检验医师', '检验医师', '检验医师', '检验 医师', '检验技师', '检验医师', '检验技师', '检验技师', '检验技师', '检验技师' ], 'gender': [ '男', '女', '女', '男', '女', '女', '女', '女', '女', '女', '女', '男', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女' 41 ], 'age_code': [ 6, 5, 6, 1, 2, 1, 2, 3, 6, 2, 3, 3, 3, 2, 2, 2, 3, 6, 2, 5, 3, 1, 1, 2, 2, 1, 2 ], 'group': [ '生化', '门诊', '生化', '门诊', '生化', '微生物', '免疫', '门诊', '生化', '门诊', '微生物', '免疫', '免疫', '生化', '门诊', '微生物', '生化', '微生物', '免疫', '门诊', '微生物', '门诊', '生化', '免疫', '门诊', '门诊', '免疫' ] } staff_df = pd.DataFrame(staff_data) # 职级判断 (假设检验技师根据年龄划分职级) def determine_level(row): if row['position'] == '检验医师': return '检验医师' elif row['age_code'] == 1: return '初级检验技师' elif row['age_code'] in [2, 3]: return '中级检验技师' else: return '高级检验技师' 附录5 介绍:部分Python代码,用于求解模型三(完整代码位于) import numpy as np import pandas as pd from itertools import combinations import time from datetime import datetime # 记录开始时间 start_time = time.time() # 定义数据 staff_data = { 'ID': list(range(1, 28)), 'Position': ['检验医师', '检验医师', '检验医师', '检验技师', '检验医师', '检验技师', ' 检验医师', '检验技师', '检验医师', '检验技师', '检验技师', '检验医师', '检验医 师', '检验医师', '检验医师', '检验技师', '检验技师', '检验医师', '检验医师', '检验医 师', '检验医师', '检验技师', '检验医师', '检验技师', '检验技师', '检验技师', '检验技 42 师'], 'Gender': ['男', '女', '女', '男', '女', '女', '女', '女', '女', '女', '女', '男', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女', '女'], 'Age_Code': [6, 5, 6, 1, 2, 1, 2, 3, 6, 2, 3, 3, 3, 2, 2, 2, 3, 6, 2, 5, 3, 1, 1, 2, 2, 1, 2], 'Department': ['生化', '门诊', '生化', '门诊', '生化', '微生物', '免疫', '门诊', '生化', '门 诊', '微生物', '免疫', '免疫', '生化', '门诊', '微生物', '生化', '微生物', ' 免疫', '门诊', '微生物', '门诊', '生化', '免疫', '门诊', '门诊', '免疫'] } # 创建员工数据框 staff_df = pd.DataFrame(staff_data) # 添加生育年龄状态(20 - 45岁的女性) staff_df['Fertility_Age'] = ((staff_df['Gender'] == '女') & (staff_df['Age_Code'].isin([1, 2, 3, 4, 5]))).astype(int) # 六月工作量数据 附录6 介绍:部分Python代码,用于求解模型四(完整代码位于支撑文件) import numpy as np import pandas as pd from openpyxl import Workbook from openpyxl.styles import Font, Alignment, PatternFill from openpyxl.utils import get_column_letter # 每月标本数和收入数据 monthly_data = { "门诊组": { "标本数": [11957, 13066, 19607, 14608, 16579, 14618, 13976, 13916, 13743, 13842, 12259, 12515], "总收入": [741790, 628135, 1113670, 752810, 877650, 771250, 717200, 686810, 705550, 713250, 608170, 764390] }, "免疫组": { "标本数": [5708, 7326, 8686, 7348, 8851, 7873, 7484, 7597, 7140, 6094, 6790, 6012], "总收入": [889290, 1355680, 1545000, 1336530, 1620690, 1408420, 1307230, 1323580, 1218260, 986550, 1024960, 878950] }, "生化组": { "标本数": [5824, 6085, 7385, 6115, 6868, 6369, 5814, 6140, 5897, 3653, 5017, 43 4861], "总收入": [751544, 801217, 943942, 791859, 905567, 800534, 771619, 761847, 727488, 587786, 591297, 627464] }, "微生物组": { "标本数": [2153, 1756, 2331, 2031, 2377, 2495, 2334, 2184, 1937, 1508, 1736, 1862], "总收入": [206871, 193897, 243934, 224887, 249603, 260591, 251123, 237868, 205905, 174168, 193830, 191744] } } # 直接使用提供的试剂成本数据 reagent_costs = { "门诊组": 168348, "免疫组": 488079, "生化组": 230747, "微生物组": 56540 }